How did newton derive formula for gravity
How did Newton derive formula for Gravitational force
F=G m1m2 / r²?
It can be proved using Kepler’s laws of planetary motion
Johannes Kepler a German astronomer had given 3 vital laws of planetary motion
All planets are revolving in an elliptical orbit. But for simplicity let’s assume it
to be circular and assume that the mass of the planet is m.
We know that speed = distance / time => time = distance / speed
Distance represented by the orbit = circumference of orbit = 2πr and so time period
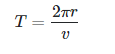
where v is the velocity. ————-(1)
We use Kepler’s law of period for proving Newton’s law of gravity.
According to Kepler, square of time period T of orbit of any planet around
the sun is directly proportional to cube of radius of it’s orbit and thus
T^2 is directly proportional to r^3 => 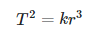 ——————–(2)
——————–(2)
Combining equations 1 & 2 we get
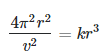 ——–(3)
——–(3)
Since the planet is following a circular orbit, it will have a centripetal acceleration
which is directed towards the center of the circle. We know that centripetal acceleration
is given by :-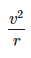 ——— (we will derive this formula in another thread)
——— (we will derive this formula in another thread)
Again as per Newton’s law we know that Force = mass * acceleration = > F = ma;
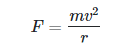 ——– (4)
——– (4)
From equations 3 & 4, we get:- 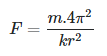 ——————(5)
——————(5)
From equation 5, we can deduce that 4π^2/k is constant and thus
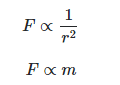
Every body in the universe exerts a force of gravity on another body and so, if we consider the solar system, the sun with mass M will also exert a force of gravity on the planet with mass m i.e. both will affect each other with a force of gravity.
Thus, force on the planet due to the sun = force on the sun due to the planet.
If the force is proportional to the mas of the planet, it should be proportional to the mass of the sun.
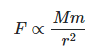 =>
=> 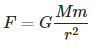
where G is the constant of proportionality called universal gravitational constant with value:- 6.674 08 x 10-11 m3 kg-1 s-2