How to prove RMS value of sine wave is peak value divided by square root 2
Consider the below sine wave:-
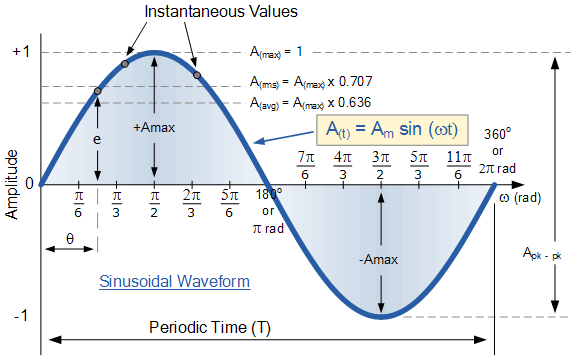
We know that sine wave is in simple harmonic motion and the amplitude at at point in time is given by Amax = A.sin(ωt) where ω is angular velocity given by 2π / T , where T is the periodic time marked by one complete crest and trough of the wave which equals 2π radian.
RMS stands for root mean square and it equals square root if the summation of squares of all the values on the waveform.
Which is given by the below formula in general:-
The same can be represented using integral calculus as below (all over time):-

But since we are considering only one crest and trough to represent peak and RMS value over time Period T, the limit to
infinity can be ignored !!
Where f(t) represents the intermediate values on the wave and frms is the root mean square value.
We know that in SHM, the value f(t) = a sin(ωt) . Substituting the value of f(t) in equation 1 we get
square of RMS value = 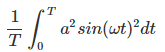 ——————————-(2) (by squaring both sides of equation 1)
——————————-(2) (by squaring both sides of equation 1)
But square of sin(ωt) =  because
because 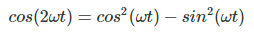 ———–(3)
———–(3)
From equations 2 and 3 we get:-
square of RMS value = 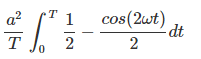 =
= =
=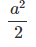
because sin (nπ) = 0—————————– (4)
From equation 4 we have RMS value = 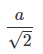 where a is the amplitude a.k.a peak value. Hence proved !!
where a is the amplitude a.k.a peak value. Hence proved !!
