How to prove volume of sphere is 4/3 × π × r³
We know that volume of sphere is v = × π × radius³
Or, v = × π × r³
Below is the proof:-
So, From the figure of sphere below
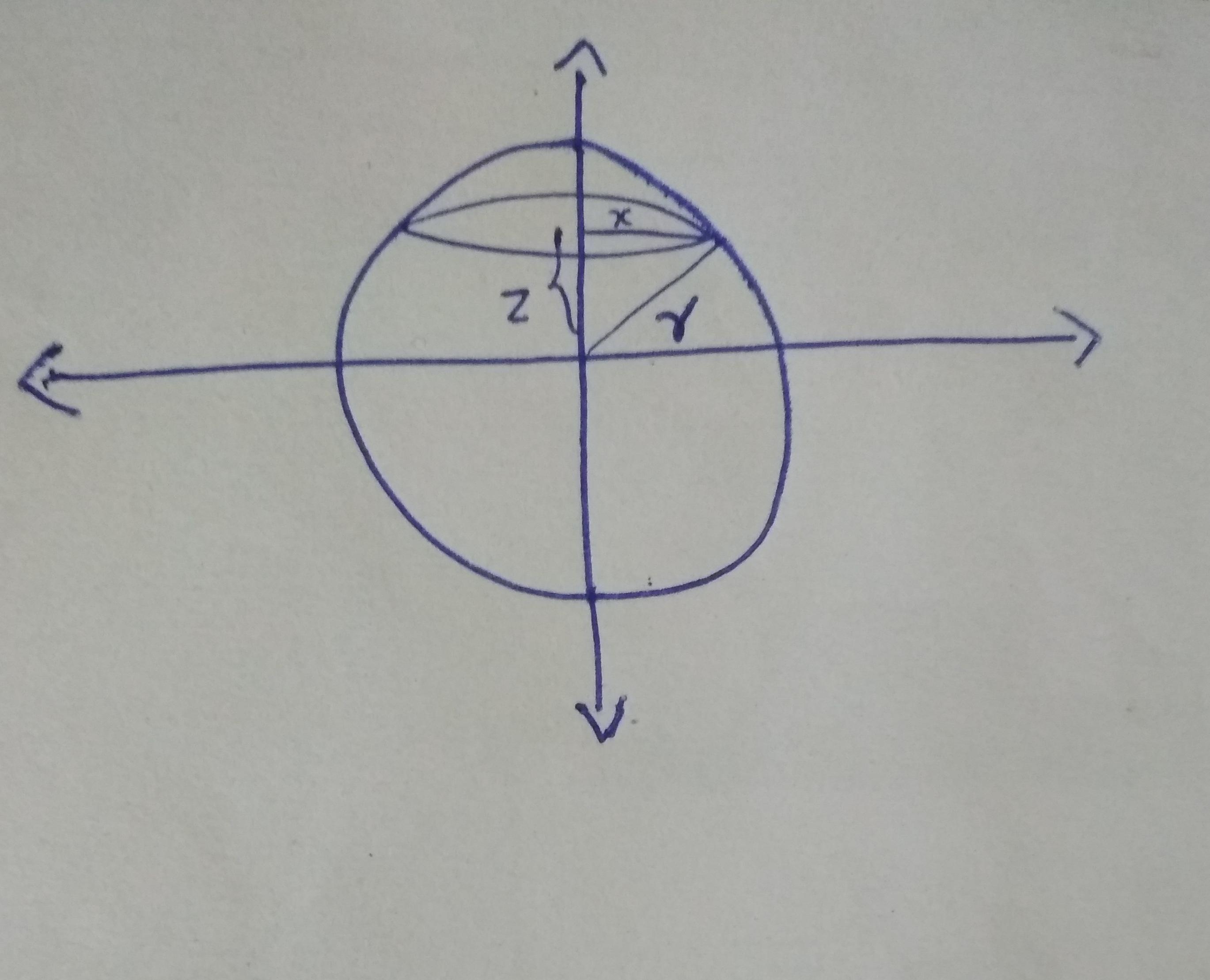
At the height of z , there is shaded disk with radius x
Let Find the area of triangle with side x , z , r
Using Pythagoras’ theorem
x² + z² = r²
Or, x² = r² – z²
Or, x =
Now, Area of shaded disk = Area = π × x²
Where x is the radius of disk
Or, Area of shaded disk = π × () ²
∴ Area of shaded disk = π × (r² – z²)
Again
If we calculate the area of all horizontal disk, we can get the volume of sphere
So, we simply integrate the area of all disk from – r to + r
i.e volume =
Or, v = – –
Or, v = π r² (r + r) – π
Or, v = π r² (r + r) – π
Or, v = 2πr³ – π
Or, v = 2πr³ ()
Or, v = 2πr³ ×
∴ v = × π × r³
Hence, The volume of radius is × π × radius³ is proved