How will you prove the below identiy ?
Using inscribed angle theorem we get:-
2B = sum of measure of arcs (AE+ED+DC)
2E = sum of measure of arcs (AB+BC+CD)
2C = sum of measure of arcs(BA+AE+ED)
since sum of measure of all arcs in a circle is 360 degrees.
=> (B+E) = (2CD+AB+BC+AE+ED) = 0.5(360+ CD)
=> (C+E) = (2AB+AE+ED+BC+CD) = 0.5(360 + AB)
Taking sin of both sides
sin(B+E) = sin (180+CD/2) = -sin(CD/2)
sin(C+E) = sin (180+AB/2) = -sin(AB/2)
sin(B+E) -sin(CD/2)
=> ________ = ___________ ——————————-(1)
sin(C+E) -sin(AB/2)
By applying cosine rule on the constructed triangles OCD an OAB, we get:-
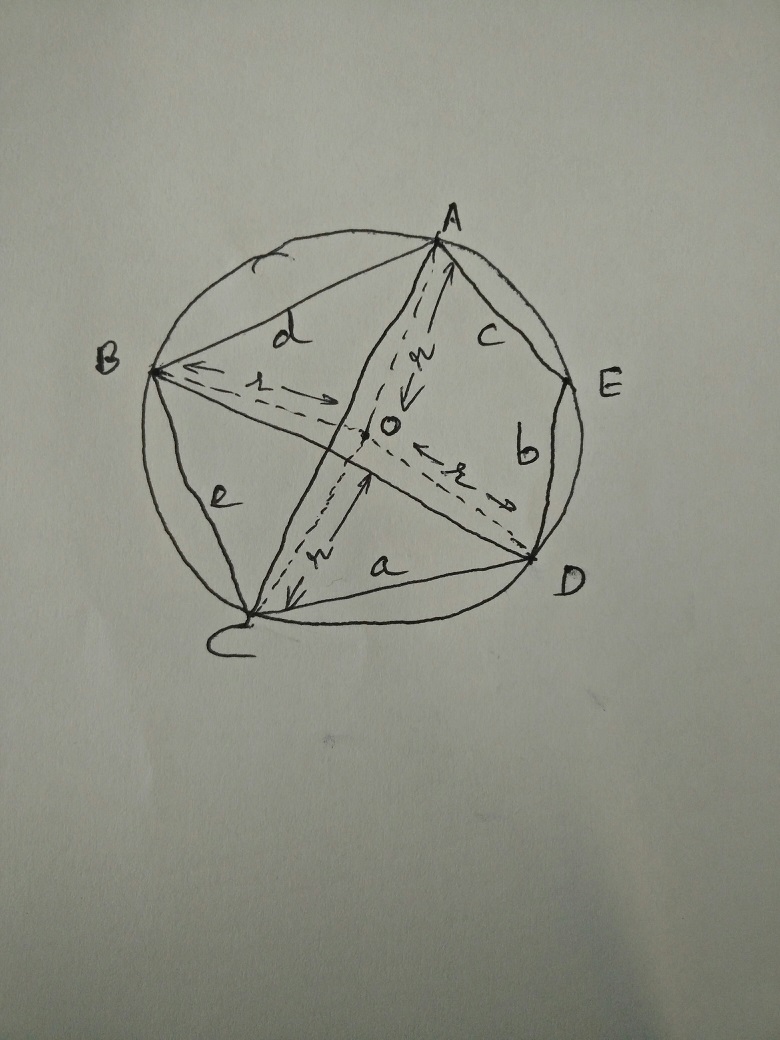
a^2 = 2*r*r – 2*r*r cos (measure of arc CD) = 2*r*r(1 – cos (measure arc CD)) ———— (2)
d^2 = 2*r*r – 2*r*r cos (measure of arc AB) = 2*r*r(1 – cos (measure arc AB)) —————-(3)
Dividing equation (2) by (3) and taking square root of both sides (considering negative value of the square root only to substitute in equation 1)
a sqrt(1 – cos CD)
__ = ___________________
d sqrt(1 – cos AB)
sqrt(1 – (1 – 2*sin^2 CD/2))
= _____________________________________
sqrt(1 – (1 – 2*sin^2 CD/2))
sqrt(2) * -sin(CD/2)
= ______________________ ——————————-(4)
sqrt(2) * -sin(AB/2)
FROM EQUATIONS 1 AND 4 we get:-
sin(B+E) a
________ = ______
sin(C+E) d
