How to prove formula for volume of cone ?
As seen in the below image, the cone is divided into 2 triangles which can be proved similar by AA test.
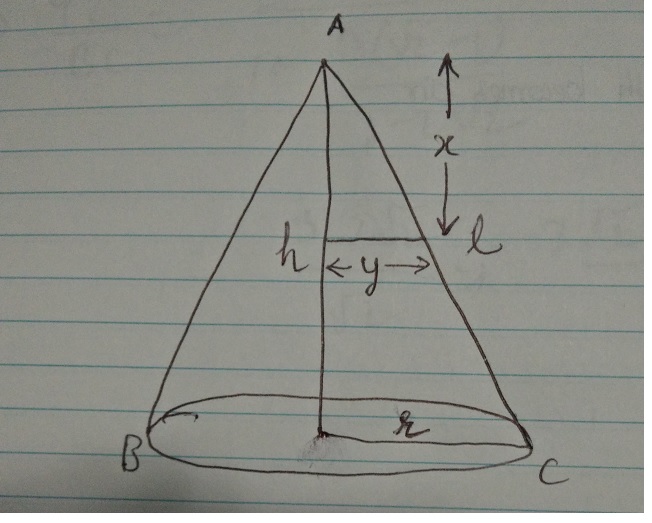
l is the slant height of the cone, r is the radius
y is the radius of the disc on the smaller triangle with x as height
Using similarity
r h rx
__ = ______ => y = ________
y x h
By integration its easy to see that volume of cone is summation of smaller discs with area
integrated over the interval 0 to h
Volume of cone =
=>
=>
=>
=>
=>
Hence proved, volume of cone is =
goli202084 Edited answer