What’s the minimum number of weights required to count between 1 to 121 pounds ?

Find the minimum number of weights required to count anything between 1 to 121 pounds ?
This type of problems have a standard formula to compute the minimum number of weights and it’s given by Ceiling of the log to the base 2 of the maximum weight to be counted.
Thus, the formula would be 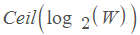 where W is the max weight which is 121 pounds in this case which would give a value of 7.
where W is the max weight which is 121 pounds in this case which would give a value of 7.
Hence the minimum number of weights required for this would be 7 and those weights would be powers of 2 from 0 until N where N will be the value such that 2^N doesn’t exceed 121, which gives the weights as [1, 2, 4, 8, 16, 32, 64]
Below is an algorithm to count all possible weights from 1 to 121 pounds using binary search.
init();
function init() {
var output = [];
var weights = [1, 2, 4, 8, 16, 32, 64];
var maxWeightToCount = 121;
for (var i = 1; i <= maxWeightToCount; i++) {
searchWeights(weights, i, output);
console.log('Sequence of minimum number of weights with sum equal = ', i,
'pounds from the given list of available weights ', weights, '=', output);
output = [];
}
}
function searchWeights(arr, value, result) {
var val = binSearch(arr, value);
if (value - val === 0) {
result.push(val);
return;
}
if (val === -1) {
val = getNearestValue(arr, value);
result.push(val);
}
searchWeights(arr, value - val, result);
}
function binSearch(arr, W, bounds=[]) {
var l = 0, r = arr.length - 1;
while (l <= r) {
var m = Math.floor(l + (r - l) / 2);
// Check if W is present at mid
if (arr[m] == W)
return arr[m];
// If W is greater, ignore left half
if (arr[m] < W)
l = m + 1;
// If W is smaller, ignore right half
else
r = m - 1;
}
bounds[0] = l, bounds[1] = r;
return -1;
}
function getNearestValue(a, value) {
var bounds = [];
if(value < a[0]) {
return a[0];
}
if(value > a[a.length-1]) {
return a[a.length-1];
}
var retVal = binSearch(a, value, bounds);
var lo = bounds[0], hi = bounds[1];
if (retVal === -1) {
retVal = (a[lo] - value) < (value - a[hi] && a[lo] < value) ? a[lo] : a[hi];
}
return retVal;
}
Explanation:-
- Use binary search to find if the weight to be counted is there in the available list of weights. If a match is found, push it to the output array and return.
- If the previous step fails, find the closest possible value from the given set of weights which is lower than the weight to be counted and push that to an array.
- Compute the difference between, intended weight to be counted and the closest possible lower value obtained in step 2 and repeat steps 1 & 2.
- Repeat step 3 until the difference obtained in step 3 is zero.
Here is the demo of the above algorithm:- http://code.golibrary.co/EjXBOJn1O72e